MATLAB编程基础
发表时间：2022-03-25来源：网络
注意：本实验报告基于MATLAB2018b版本；
一、绘图：
1．在同一图形窗口画出下列两条曲线图像并标注：y1=2x+5；y2=x^2-3x+1。
源代码：
x=-10:0.01:10; y1=2*x+5; y2=x.^2-3*x+1; plot(x,y1,'r',x,y2,'b'); xlabel('x') ylabel('y1&y2') legend('y1=2x+5','y2=x^2-3x+1') grid on实验结果：
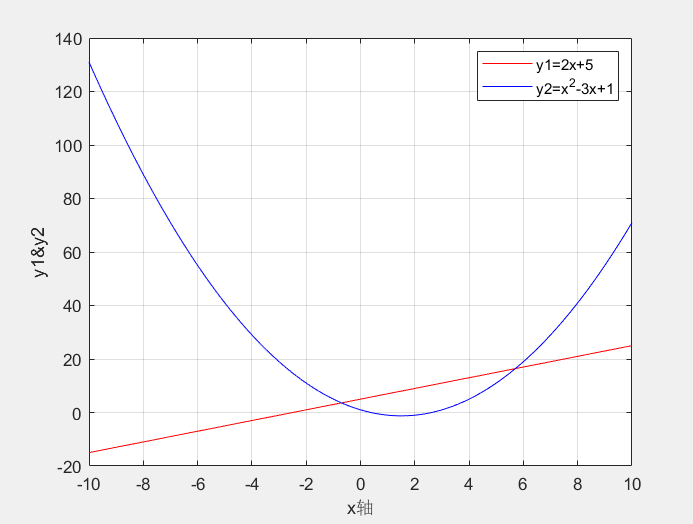
分析：plot函数可以一次绘制多条曲线，legend用于添加图例。
2. 画出下列函数的曲面及等高线。
源代码：
[x,y]=meshgrid(-10:0.1:10); z=x.^2+y.^2+sin(x*y); subplot(2,1,1) mesh(x,y,z) subplot(2,1,2) colormap([0.6 0.5 1]) contour(x,y,z,20)实验结果：
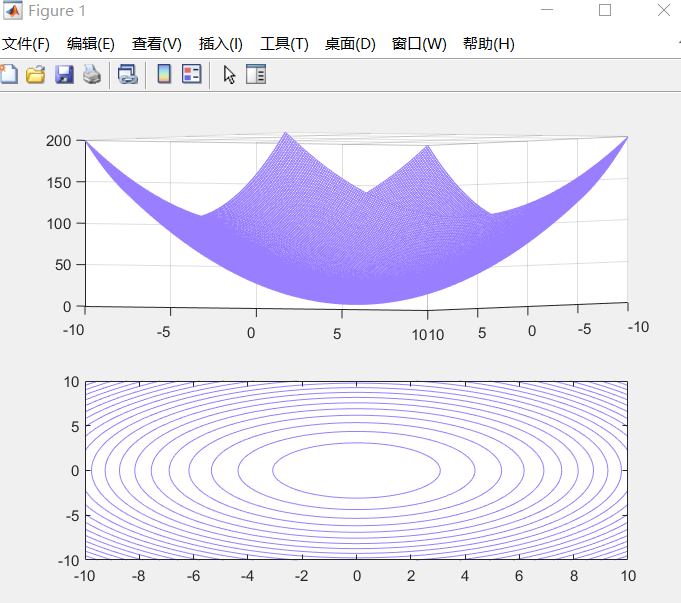
分析：contour用于绘制等值线。
二、程序设计：
3. 编写程序计算（x在[-3，3]，间隔0.01）
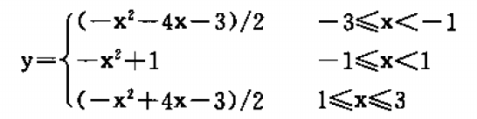
源代码：
x=input('Enter value of x:'); if x>=-3&&x=-3&&x=1&&x分析：input为输入一个常量函数，fprintf用于输出，disp也用于输出。
4．有一列分数序列：求前15项的和。
分析：zeros(m,n)用于创建一个m*n的零矩阵，ones(m,n)同。
5.是否任意3的倍数m可以写成三个素数p1、p2、p3的和（试着写出所有的m=p1+p2+p3的可能形式）？
源代码：
m=input('请输入任意一个数（3的倍数）:'); if mod(m,3) error('应输入一个3的倍数') elseif m分析：error可以用于提示错误信息。
三、数据处理与拟合初步：
6．通过测量得到一组数据：
t： 1 2 3 4 5 6 7 8 9 10
y：4.842 4.362 3.754 3.368 3.169 3.038 3.034 3.016 3.012 3.005
分别采用y=c1+c2e^(-t)和y=d1+d2te^(-t)进行拟合，并画出拟合曲线进行对比。
源代码：
t=1:10; y=[4.842 4.362 3.754 3.368 3.169 3.038 3.034 3.016 3.012 3.005]; p1=polyfit(exp(-t),y,1); xt1=1:0.5:10; yt1=polyval(p1,exp(-xt1)); subplot(2,1,1) plot(t,y,'ro',xt1,yt1,'b') legend('数据点','exp(-t)拟合') p2=polyfit(t.*exp(-t),y,1); xt2=1:0.5:10; yt2=polyval(p2,xt2.*exp(-xt2)); subplot(2,1,2) plot(t,y,'ro',xt2,yt2,'b') legend('数据点','t*exp(-t)拟合')实验结果：
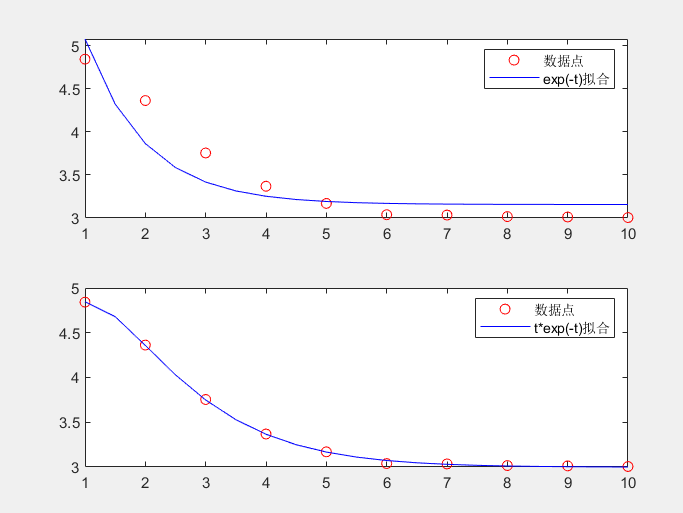
分析：polyfit用于多项式数据拟合。
7．计算下列定积分
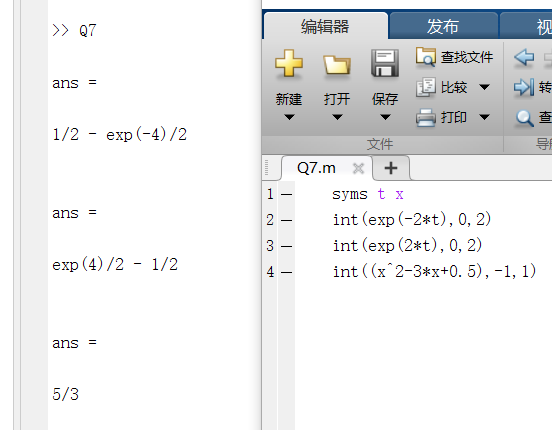
分析：syms用于申明变量，int()用于求解积分，参数分别是被积函数、积分下限和积分上限。
8．微分方程组
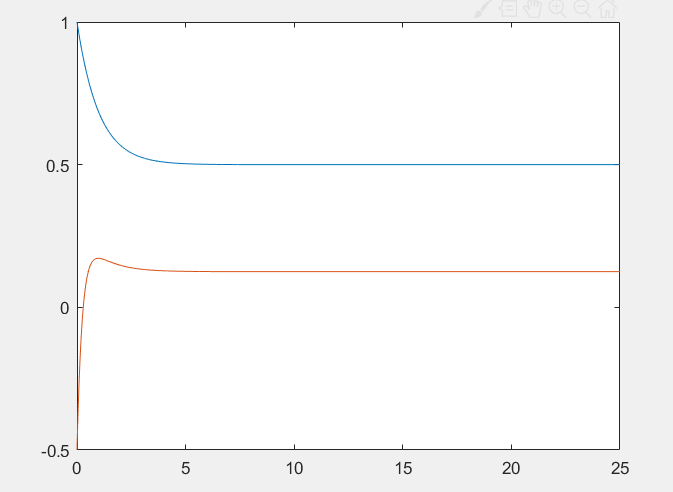
分析：dsolve函数用于求解微分方程。
9．设通过测量得到时间t与变量y的数据：
t=[0 0.3 0.8 1.1 1.6 2.3];y=[0.5 0.82 1.14 1.25 1.35 1.41];
分别采用多项式：y=a0+a1t+a2t^2和指数函数：y=b0+b1e^t+b2te^t进行拟合，并计算均方误差、画出拟合效果图进行比较。
源代码：
t=[0 0.3 0.8 1.1 1.6 2.3]; y=[0.5 0.82 1.14 1.25 1.35 1.41]; p1=polyfit(t,y,2); xt1=1:0.01:2.3; yt1=polyval(p1,xt1); z1=polyval(p1,t); wuchal=sqrt(sum(z1-y).^2); subplot(2,1,1) plot(t,y,'ro',xt1,yt1,'b') legend('数据点','y=a0+a1t+a2t^2拟合','location','southeast') p2=polyfit(exp(-t),y,2); xt2=1:0.01:2.3; yt2=polyval(p2,exp(-xt2)); z2=polyval(p2,t); wucha2=sqrt(sum(z2-y).^2); subplot(2,1,2) plot(t,y,'ro',xt2,yt2,'b') legend('数据点','y=b0+b1e^t+b2te^t','location','southeast')实验结果：
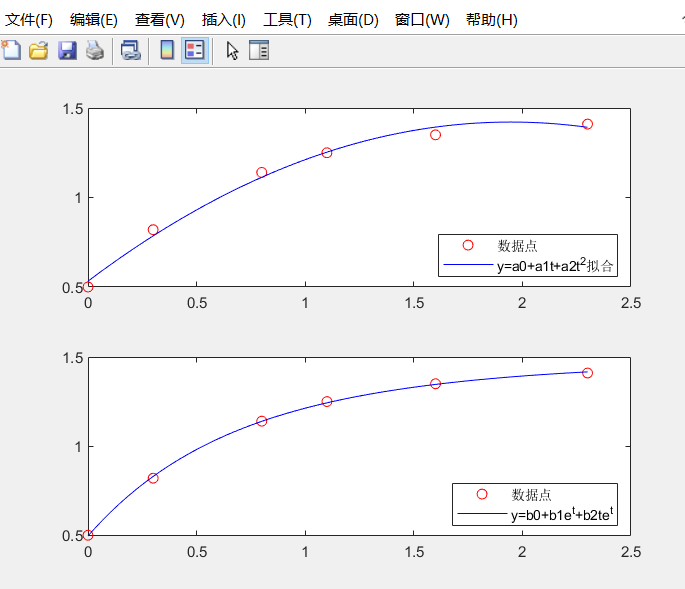
分析：polyval用于评估多项式。
10．观察函数：y=e^x-1.5cos(2*pi*x)在区间[-1,1]上的函数图像，完成下列两题：
用函数fzero求解上述函数在[-1,1]的所有根，验证你的结果；源代码：
x=-1:0.1:1; y=exp(x)-1.5*cos(2*pi*x); y0=0; plot(x,y,'b',x,y0,'r*'); fun=@(x) exp(x)-1.5*cos(2*pi*x); x1= fzero(fun,-0.8) x2= fzero(fun,0) x3= fzero(fun,0.8) xlabel('X'); ylabel('Y');实验结果：
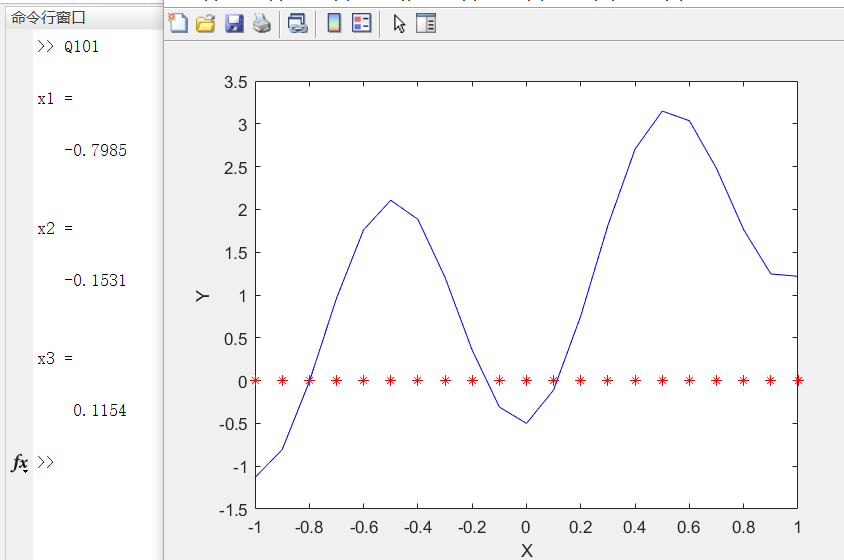
（2）用函数fminbnd求解上述函数在[-1,1]上的极小、极大、最小和最大值，在函数图像上标出你求得的最小值点作出验证。
注：可以用help fzero命令查看fzero的调用格式，fminbnd典型的调用方法是：fminbnd(@myfun,x1,x2) %返回函数myfun在区间[x1,x2]上的。
源代码：
disp('函数在区间[-1,1]:'); %求极小值 fun1=@(x)exp(x)-1.5*cos(2*pi*x); [xmin1,ymin1]=fminbnd(fun1,-0.2,0.2); disp(['极小值坐标为:(' num2str(xmin1),',',num2str(ymin1),')']); %求极大值 fun2=@(x)(-(exp(x)-1.5*cos(2*pi*x))); [xmax1,ymax1]=fminbnd(fun2,-1,-0.2); [xmax2,ymax2]=fminbnd(fun2,0.2,1); disp(['极大值坐标为:(' num2str(xmax1),',',num2str(-ymax1),')和(',num2str(xmax2),',',num2str(-ymax2),')']); % 求最小值 ymin = fun1(1); if ymin>fun1(-1) ymin = fun1(-1); end if ymin>ymin1 ymin=ymin1; end disp(['最小值为:',num2str(ymin)]) % 求最大值 ymax = fun1(1); if ymax(-ymax2) ymax3=-ymax1; end if ymax感谢您的观看，查看更多精彩内容请关注微信公众“理工科日记”。
上一篇：Python
知识阅读
软件推荐
更多 >-
查看溧阳论坛触屏版手机版下载v5.4.2.18 安卓版
68.37MB |生活服务
-
查看保利悠悦荟最新版app2026下载v3.1.6 安卓版
35.73MB |生活服务
-
查看i泰达官方版下载v2.0.10 安卓版
66.01MB |生活服务
-
查看与糖医护手机版下载v4.2.0 安卓版
46.54MB |生活服务
-
查看智慧宫翻译阿拉伯语手机版下载v1.91.0 安卓版
50.68MB |生活服务
-
查看专注清单app下载v15.9 安卓版
42.61MB |生活服务
-
查看物性表手机版下载v2.3.0 安卓版
71.12MB |商务办公
-
查看hooli留学公寓app下载v5.6.1 安卓官方版
28.64MB |生活服务
-
1
-
2
盖瑞模组机器人下载v1.66.1 安卓版
其它手游 -
3
狂飙大卡车下载v1.0.7 安卓版
其它手游 -
4
海洋连连消下载v1.0.7 安卓版
其它手游 -
5
来切我呀下载v1.1.1 安卓版
其它手游 -
6
猎手大追捕下载v187.1.1 安卓版
其它手游 -
7
疯狂牛马实验室下载v2.0.1 安卓版
其它手游 -
8
炮弹消消乐下载v0.251111.169 安卓版
其它手游 -
9
极限躲猫猫模拟下载v1.0 安卓版
其它手游 -
10
尸群突袭最新版下载v3 安卓版
其它手游
