经典排序算法总结（含JAVA代码实现）

发表时间：2022-03-26来源：网络

0、排序算法说明

0.1 排序的意义

对一序列对象根据某个关键字进行排序

0.2 术语说明

稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面； 不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面； 内排序：所有排序操作都在内存中完成； 外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行； 时间复杂度： 一个算法执行所耗费的时间。 空间复杂度：运行完一个程序所需内存的大小。

0.3 算法总结

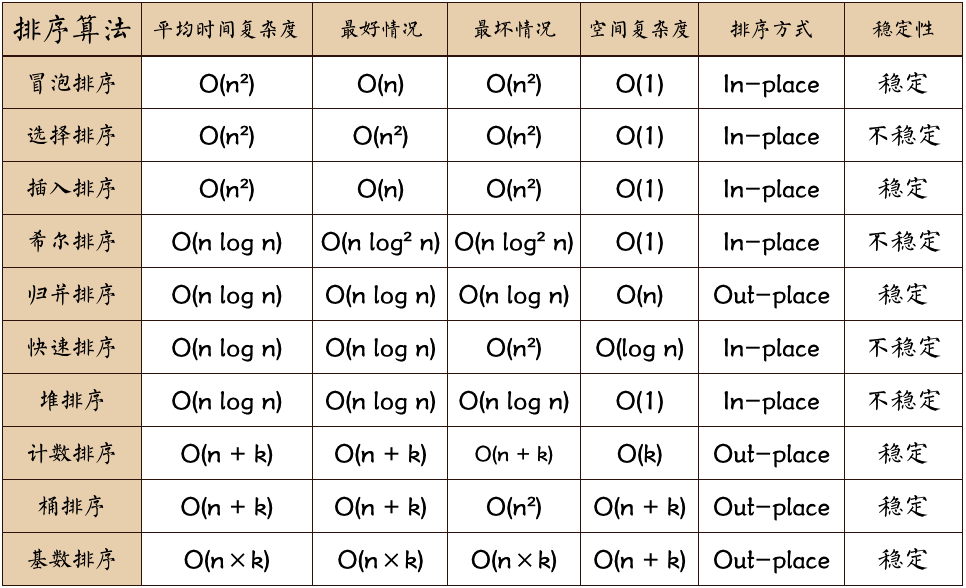
图片名词解释：

n: 数据规模 k: “桶”的个数 In-place: 占用常数内存，不占用额外内存 Out-place: 占用额外内存

0.5 算法分类

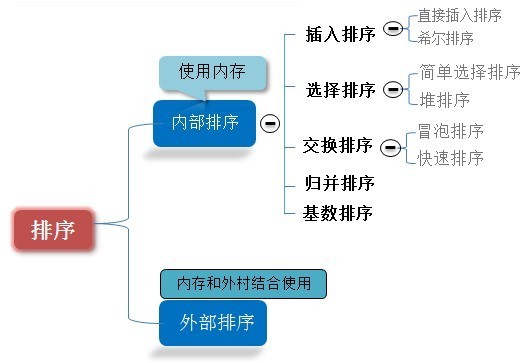
0.6 比较和非比较的区别

常见的快速排序、归并排序、堆排序、冒泡排序等属于比较排序。在排序的最终结果里，元素之间的次序依赖于它们之间的比较。每个数都必须和其他数进行比较，才能确定自己的位置。
在冒泡排序之类的排序中，问题规模为n，又因为需要比较n次，所以平均时间复杂度为O(n²)。在归并排序、快速排序之类的排序中，问题规模通过分治法消减为logN次，所以时间复杂度平均O(nlogn)。
比较排序的优势是，适用于各种规模的数据，也不在乎数据的分布，都能进行排序。可以说，比较排序适用于一切需要排序的情况。

计数排序、基数排序、桶排序则属于非比较排序。非比较排序是通过确定每个元素之前，应该有多少个元素来排序。针对数组arr，计算arr[i]之前有多少个元素，则唯一确定了arr[i]在排序后数组中的位置。
非比较排序只要确定每个元素之前的已有的元素个数即可，所有一次遍历即可解决。算法时间复杂度O(n)。
非比较排序时间复杂度底，但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求。

1、冒泡排序（Bubble Sort）

冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

1.1 算法描述

比较相邻的元素。如果第一个比第二个大，就交换它们两个；对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；针对所有的元素重复以上的步骤，除了最后一个；重复步骤1~3，直到排序完成。

1.2 动图演示

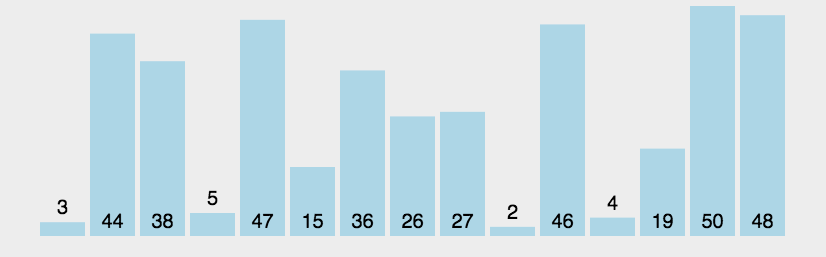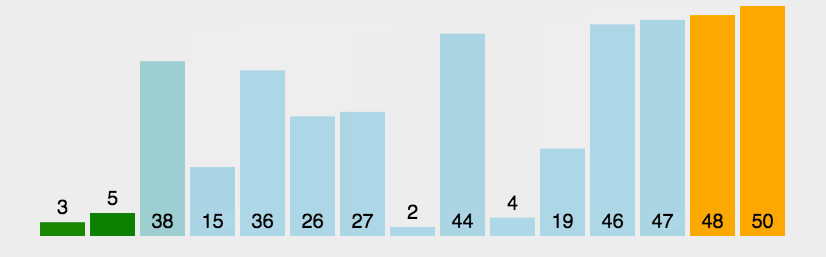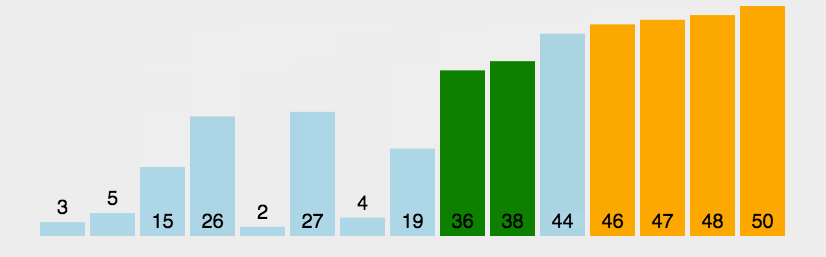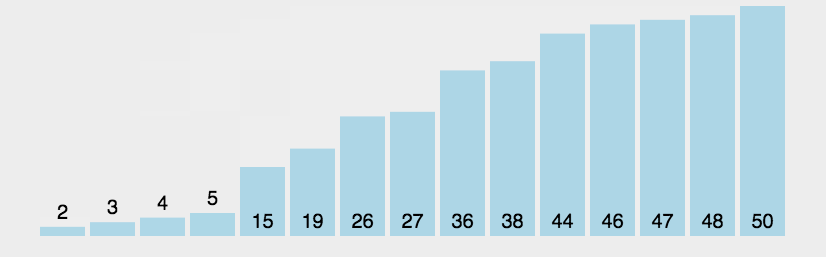
1.3 代码实现

/** * 冒泡排序 */ public static int[] bubbleSort(int[] array){ if (array.length == 0) return array; for (int i = 0; i < array.length; i++){ for (int j = 0; j < array.length - 1 - i; j++){ if (array[j+1] = 0 && current tj，tk=1；按增量序列个数k，对序列进行k 趟排序；每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

4.2 过程演示

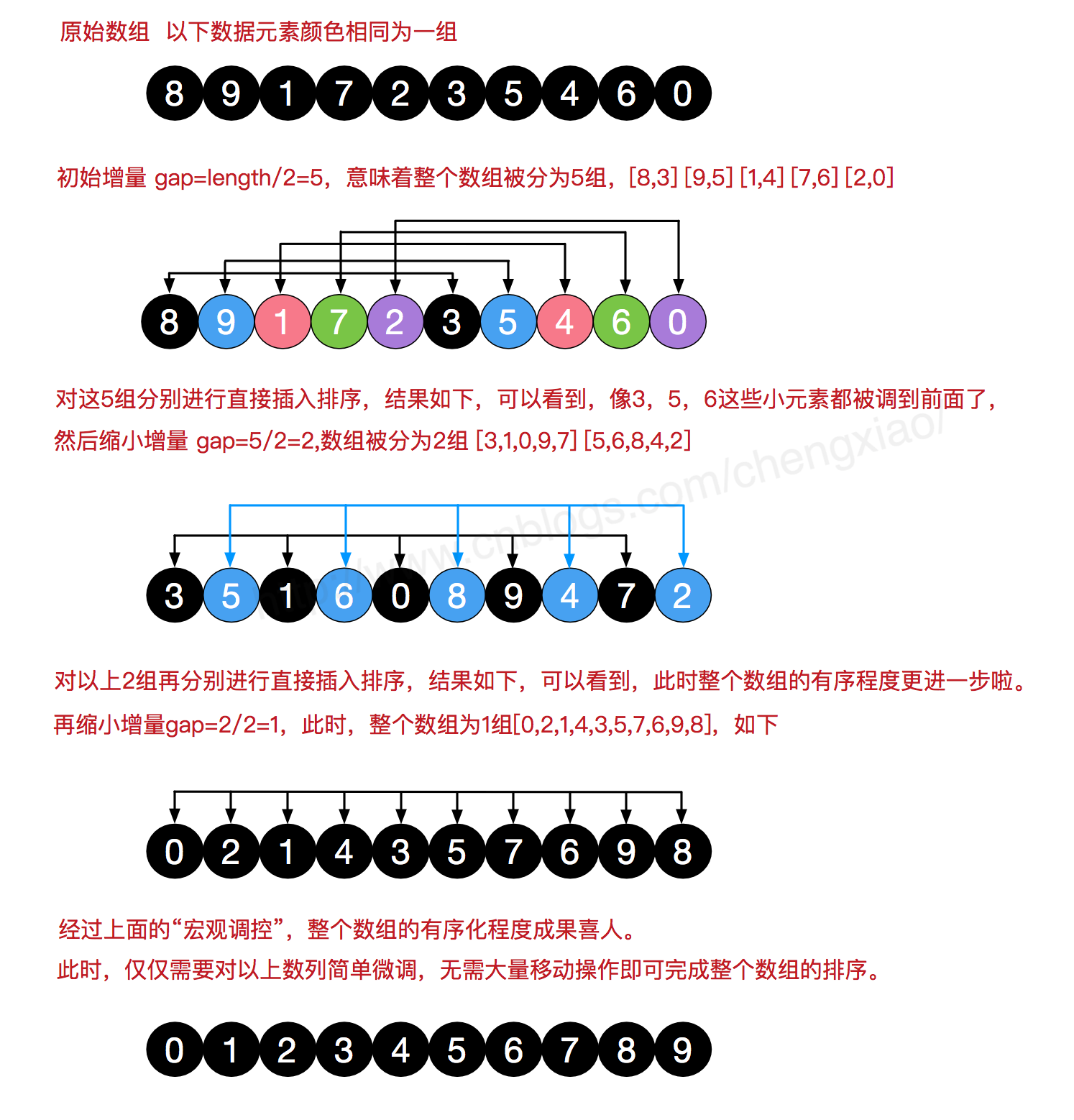
4.3 代码实现

/** * 希尔排序 */ public static int[] ShellSort(int[] array){ int len = array.length; int temp, gap = len / 2; while (gap > 0){ for (int i = gap; i < len; i++){ temp = array[i]; int preIndex = i - gap; while (preIndex >= 0 && array[preIndex] > temp){ array[preIndex + gap] = array[preIndex]; preIndex -= gap; } array[preIndex + gap] = temp; } gap /= 2; } return array; }

4.4 算法分析

最佳情况：T(n) = O(nlog2 n)

最坏情况：T(n) = O(nlog2 n)

平均情况：T(n) =O(nlog2n)

5、归并排序（Merge Sort）

和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是O(n log n）的时间复杂度。代价是需要额外的内存空间。

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

5.1 算法描述

把长度为n的输入序列分成两个长度为n/2的子序列；对这两个子序列分别采用归并排序；将两个排序好的子序列合并成一个最终的排序序列。

5.2 动图演示

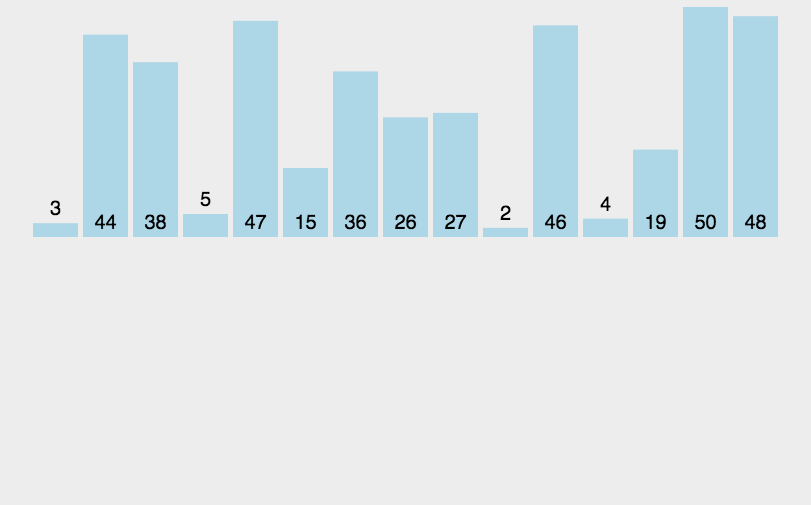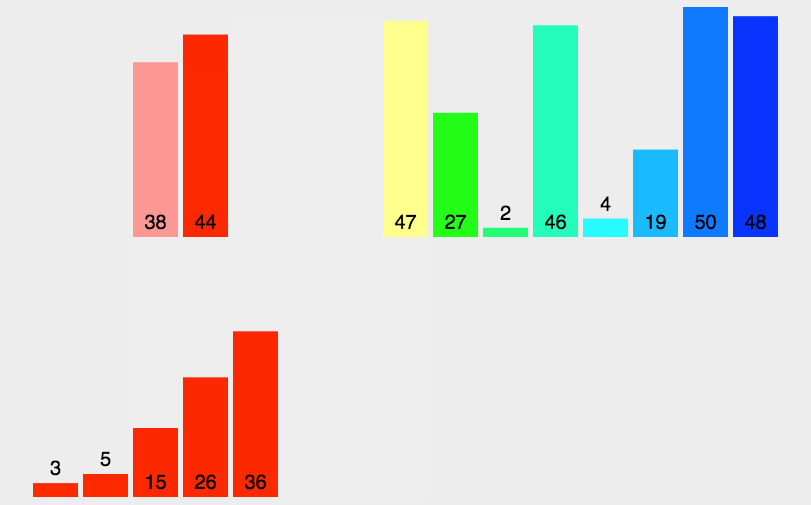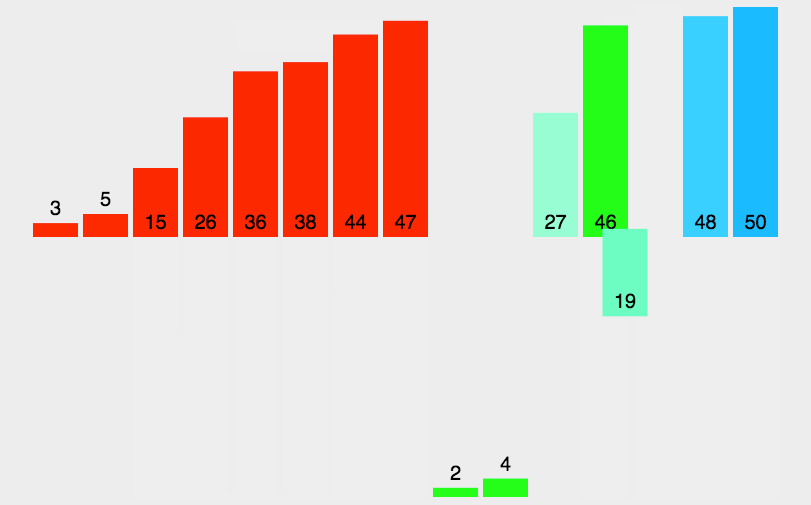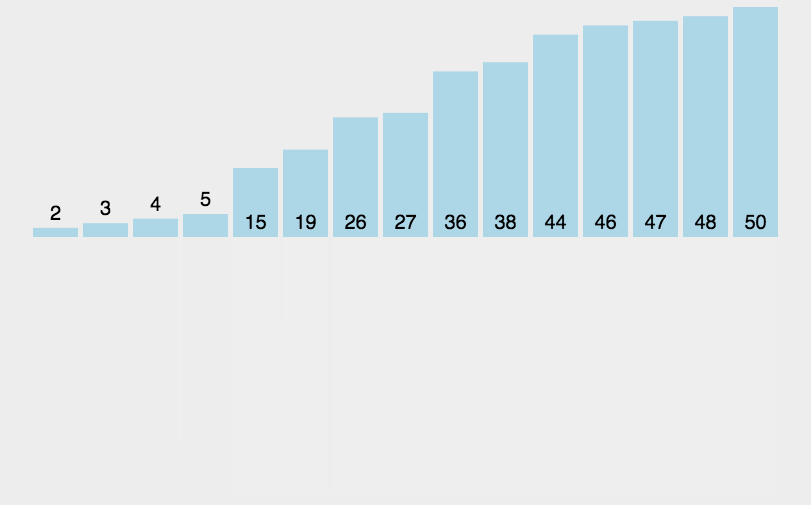
5.3 代码实现

/** * 归并排序 */ public static int[] MergeSort(int[] array){ if (array.length < 2) return array; int mid = array.length / 2; int[] left = Arrays.copyOfRange(array, 0, mid); int[] right = Arrays.copyOfRange(array, mid, array.length); return merge(MergeSort(left), MergeSort(right)); } /** * 归并排序——将两段排序好的数组结合成一个排序数组 */ public static int[] merge(int[] left, int[] right){ int[] result = new int[left.length + right.length]; for (int index = 0, i = 0, j = 0; index < result.length; index++){ if (i >= left.left) result[index] = right[j++]; else if (j >= right.length) result[index] = left[i++]; else if (left[i] > right[j]) result[index] = right[j++]; else result[index] = left[i++]; } return result; }

5.4 算法分析

最佳情况：T(n) = O(n)

最差情况：T(n) = O(nlogn)

平均情况：T(n) = O(nlogn)

6、快速排序（Quick Sort）

快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

6.1 算法描述

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

从数列中挑出一个元素，称为 “基准”（pivot）；重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

6.2 动图演示

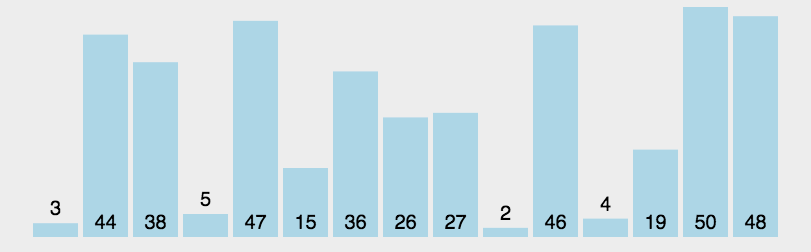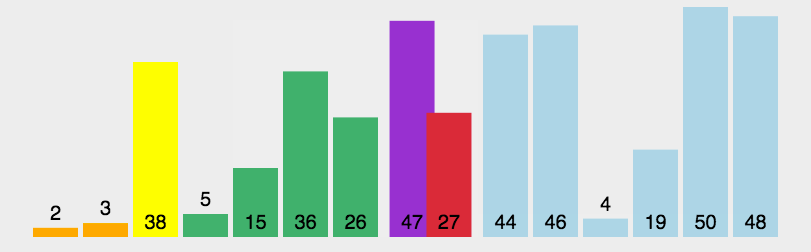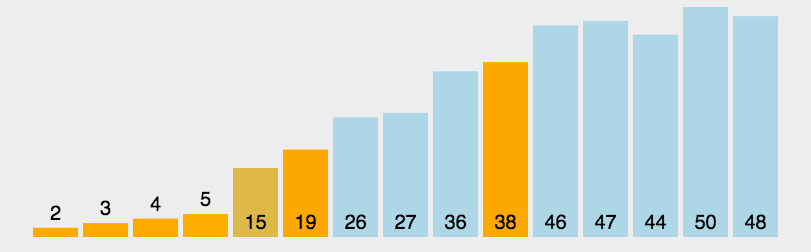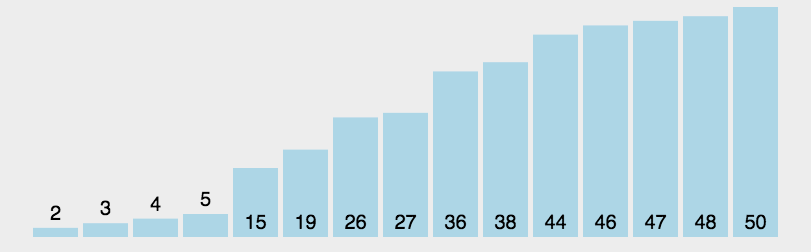
6.3 代码实现

/** * 快速排序 */ public static int getIndex(int[] arr, int low, int high){ //基准数据 int temp = arr[low]; while (low = temp){ high --; } // 如果队尾元素小于tmp了,需要将其赋值给low arr[low] = arr[high]; // 当队首元素小于等于tmp时,向前挪动low指针 while (low array[maxIndex]) maxIndex = i * 2 + 1; //如果父节点不是最大值，则将父节点与最大值交换，并且递归调整与父节点交换的位置。 if (maxIndex != i) { swap(array, maxIndex, i); adjustHeap(array, maxIndex); } }

7.4 算法分析

最佳情况：T(n) = O(nlogn)

最差情况：T(n) = O(nlogn)

平均情况：T(n) = O(nlogn)

8、计数排序（Counting Sort）

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

计数排序(Counting sort)是一种稳定的排序算法。计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。

8.1 算法描述

花O(n)的时间扫描一下整个序列 A，获取最小值 min 和最大值 max

开辟一块新的空间创建新的数组 B，长度为 ( max - min + 1)

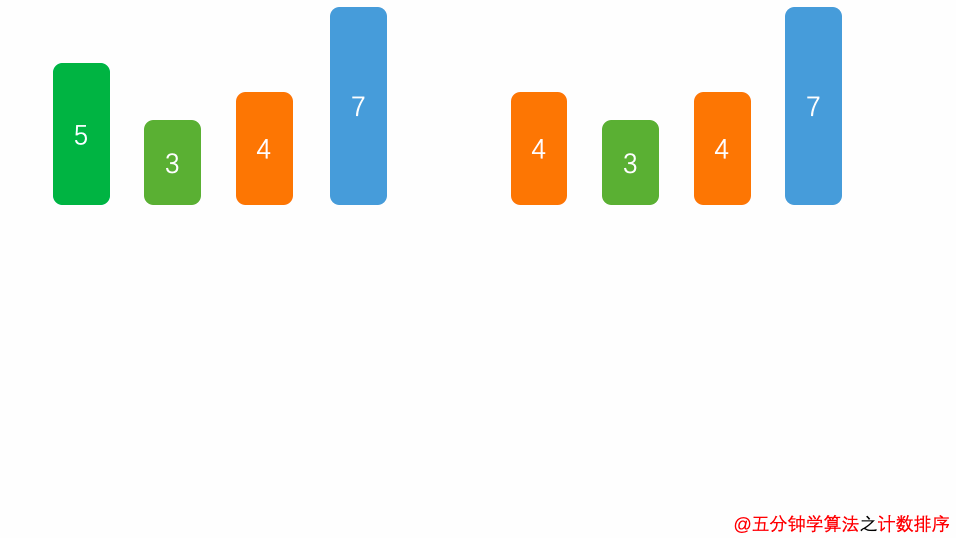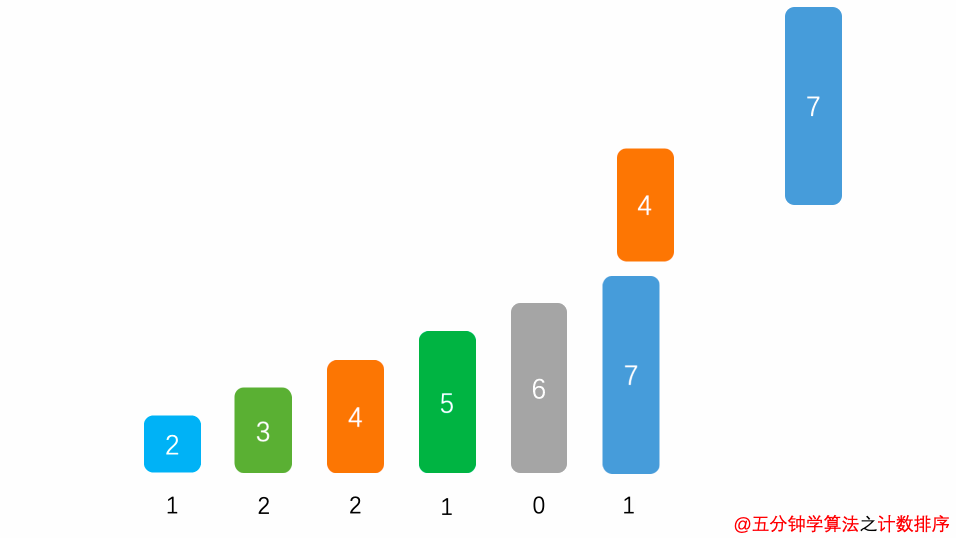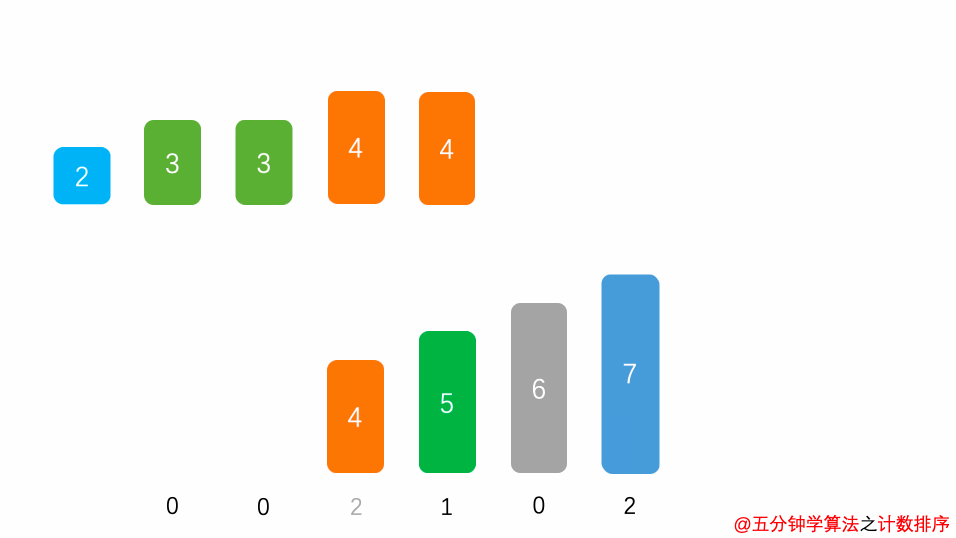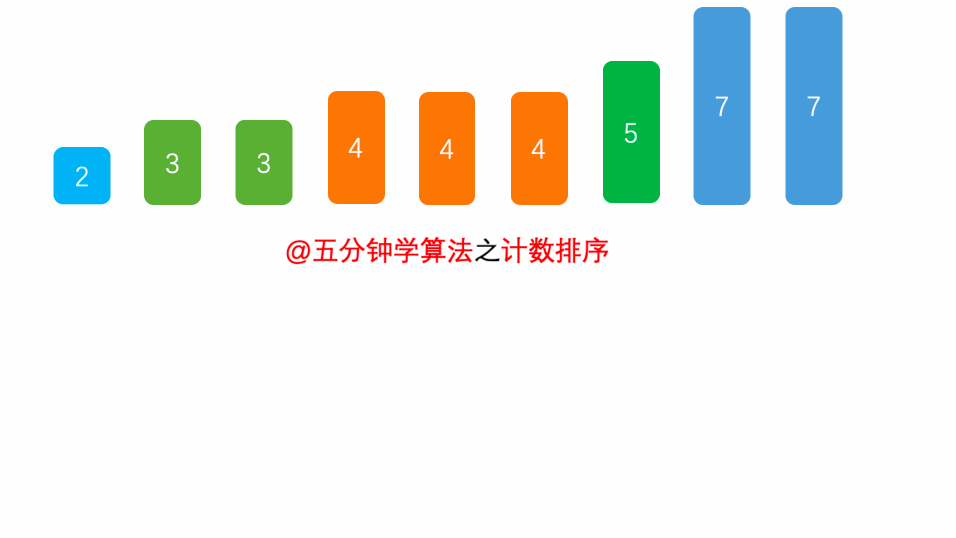
数组 B 中 index 的元素记录的值是 A 中某元素出现的次数

最后输出目标整数序列，具体的逻辑是遍历数组 B，输出相应元素以及对应的个数

8.2 动图演示

8.3 代码实现

/** * 计数排序 */ public static int[] CountingSort(int[] array) { if (array.length == 0) return array; int bias, min = array[0], max = array[0]; for (int i = 1; i < array.length; i++) { if (array[i] > max) max = array[i]; if (array[i]

上一篇：十大经典排序算法（全面总结+Java代码实现）

下一篇：java代码模板